Magnetic Field, Loop, and Faraday (21st Day)

Spring 2015

Professor Mason

May 14 Class

Magnetic Field on Wire

First thing in class, we needed to predict and draw the direction of magnetic field including the force and which direction the magnetic field is pointing at 4 location shown in the picture below. To calculate the force, we use this formula [F vector = B vector I L vector], or [F vector = (Uo I1 I2/ 2pi r) L vector], which r is the distance between two wires. Since B is perpendicular to I, we could also say that [B vector = Uo I1 I2/ 2pi r]. 

If a magnetic field on the axis of loops has a straight line wire that gives us circular magnetic field, circular wire gives us straight line magnetic field. The picture shown above also shows a B vector graph when B vector sensor is spun around the classroom (similar to wave graph); the highest point of the graph shows the north direction, while the lowest point of the graph shows the south direction. The picture attached below shows us the experiment with the wire. We were also asked if there was any force acting on the wire shown in the picture below; the answer is no, there is no force between the wires because the direction of the current is going back and forth, therefore they cancel each other out. 

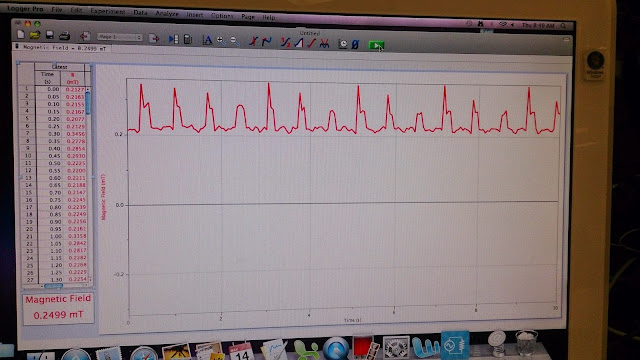
Experiment With Magnetic Field on Logger Pro.
Next, we had an experiment, which involved a power supply, test tube, copper wire, magnetic field reader, and alligator clips. The setup is shown in the picture below. In this experiment, we needed to determine how the graph of magnetic field would look like on logger pro based on how many loops encircling the test tube. We had to put the magnetic field reader close to the test tube, so that it would read accurately. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 1 and 1 loop encircling the test tube.

 The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 1 and 2 loop encircling the test tube.

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 1 and 3 loop encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 1 and 4 loop encircling the test tube.

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 1 and 5 loop encircling the test tube. 

After we were done with power supply 1, we noticed that the big difference only lies in 1 loop and 2 loops; the rest of loops did not have much of a difference than 2 loops encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 2 and 1 loop encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 2 and 2 loop encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 2 and 3 loop encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 2 and 4 loop encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 2 and 5 loop encircling the test tube. 

When using power supply 2 (shown in the picture below), we noticed from 1 loop to 5 loops, the differences are the Magnetic Field (B); the graph increases the height as we added more loops encircling the test tube.

Galvanometer

In class, we were shown this old machine called Galvanometer as shown in the picture attached above. It is used to detect current and give an analogous reading. In this experiment, there was a  loop of wire attached up to the galvanometer, and it showed 0 A because there was no current at this point of time. The professor then took a bar of magnet and placed it into the center of the loop of wire. The galvanometer then suddenly started for a second to give a reading of some current. After he pulled it out, the galvanometer would get another reading; however, this time the galvanometer gave a negative direction. The professor then did the experiment again; however, this time he moved the bar of magnet back and forth in the center of the loop at higher speed. After that, the galvanometer received a higher reading of the magnitude of the current flowing within the wire. From this experiment, we could conclude that magnetic field can generate wireless current.

Faraday's Machine

In class, we get to see a Faraday's machine. The professor told us four things that are important in using the Faraday's Machine, and those are the strength of the magnet, the velocity of magnet's entry and exit, the radius of loop coil, and number of coils. 

The first thing he put in the Faraday's machine in this experiment was a coil with light bulb attached. Then, the bulb lights up when it is in the pole. 

The bulb did not light up again after the coil is released from the pole. 

In this experiment, the professor also provided us a copper ring, aluminum ring, steel ring, and special steel ring (has a gap in between the disk); however, we did not take pictures of them; thus we knew how they worked. First, when the professor put the copper ring inside the pole, it levitated slightly upward; next, when the professor put the aluminum ring inside the pole, it levitated higher than copper ring because aluminum is lighter than copper; next, when the professor put steel ring inside the pole, it levitated as high as copper; however, when the professor put a special steel ring in the pole, it did not levitate at all because the magnetic field was interrupted by the gap between the disk, so it did not make any circular motion. After the experiment, the professor came up with another equation, which was motion EMF [E = VB] or [E vector = V/L] or [E vector = V L B vector]. 

Falling Experiment

In class, professor did another experiment with two objects; one is magnetic and the other one is not. He also prepared two tubes; one is made of plastic glass, and the other one is made of aluminum. He purposely drop two objects at the same time through different pole. The magnetic object going through the aluminum tube fell down so much slower than the other one because the object is spinning in circular current; however, it did not stop because the gravity is pulling the object down, and it needed to move to fall down.

After the experiment, the professor came up with another equation of [E = -NA (dB/dt)] or [E = N (d(B vector dot A vector)/ dt)], which E is Lenz's Law (Induced EMF) using [Magnetic Flux = B.A]. Then, the professor gave us another equation of [B = Bo Sin wt], [Flux = pi R^2 Bo Sin wt], and [E = -Npi R^2 Bo Cos wt]. These equations are used to find the flux in a coil as function of time. Next, we also needed to draw emf vs t graph based on B vs t graph; the result looks like the graph shown in the picture attached below. 

Magnetic Loop (20th Day)

Spring 2015

Professor Mason

May 12 Class

Magnetized Pin

In class, we had to draw the magnetic field of an ordinary pin and magnetized pin, and this picture attached below shows us that ordinary pin has positive and negative charges arranged randomly close to each other; while the magnetized pin has separated positive and negative charges inside the pin.

Based on the professor's lecture, we found out that when there is magnetic field, there will exist force; magnetic force is defined as an equation of [F = IL x B vector] and torque as an equation of [T = IL^2B]; thus, we could also say that [F = qv x B vector].

In class, we also learned that there are two ways to destroy magnetism in an object, and those are by heating up the object until it reaches certain temperature, and by hitting the object with a hammer. In class, the professor did an experiment with a magnetized pin; he showed us how to eliminate the magnetism in the pin by heating it up with a blowtorch shown in the picture attached below. The second way is to hit the object with a hammer; hitting the object with a hammer will cause a massive vibration to that object and will eventually lose all the magnet inside the object. 

Magnetic Loop and Torque
In class, we had to do a calculation to find the net force of a current loop and to find net torque acting on the loop. We found out that the definition of torque is R x F; we also found out the bigger loop has bigger torque.

The picture attached above shows us the calculation to find the torque of a loop and the direction of the loop. We used another equation of [T = NIAB] to find the torque. The calculations are shown in the picture above. For the direction of the loop, it would be 90 degrees because A is perpendicular to I. For the calculation shown in the picture below, we also used an equation of [T = NIAB].

Experiment with Magnet and Power Supply

In class, the professor told us that the things that most likely would make a motor to fail to work are brush, coil, and commuter. Then, we continued doing to the experiment, which involved this thing shown in the picture below. 

We needed three batteries and wire attached to this thing in order to get it working. However, before attaching all the stuff needed, we also needed to adjust the direction of the magnet. After all things had been set up, we attached the wires to the batteries in order to make the thing in the middle with copper spun; the direction of where the thing would spin depends on the direction of the magnet (North and South).

We need to determine the direction of the spin based on the magnet. First, we did North-facing magnet on the left and South-facing magnet on the right. The result is shown in the picture attached below. On the other hand, we also needed to do the other way around, which South-facing magnet would be on the left and North-facing magnet on the right. Also, nothing happened when the magnet poles on both sides are the same (North facing North and South facing South). The magnetism in this thing cancelled each other out when they are facing the same sides. 

The next experiment we did was to make the circular copper wire spin. The things we needed for this setup was a power supply, alligator clips, magnetic bar, circular copper wire, and two copper wire holders to keep the copper wire from falling. First, in order to get it working, we needed to attach the alligator clips to the power supply, and set it to 4.5 Volts; after the set up was completed, the circular copper wire would spin as shown in the picture attached below. Before the setup was completed, we had to rub one end of the copper wire with sandpaper 360 degree; for the other end of the wire, we just needed to rub it 180 degree with sandpaper; we had to do this in order to connect the wire with the power supply.

Experiment with Magnetic Pole

In this experiment, the professor put a magnetic pole in the middle, and he placed 5 compasses around the magnetic pole to see which direction the compasses are pointing. 

As shown in the picture attached below, the compasses are pointing in circular motion. The directions of the compasses depend on the flow of the current; therefore, by reversing the current flow, it reverses the direction of the compasses as well. Finally, we could conclude that B vector is perpendicular to the current, and B vector is also perpendicular to 1/r, which r is the distance from magnet to compass. 

Loop Calculation

This time, we were given a setup of a loop, and we needed to find the dB, which dB has a definition in a form of equation of [dB = (Uo/4pi) (IdI x r vector/ r^2)]. 

In this problem, we also found out a new equation, and that is [Fb/Fe = Eo Uo V^2], which could be simplified as [Fb/Fe = V^2/C^2]. In this calculation, we were given that Uo and Eo are constants, which are [Uo = 1.25x10^-6] and [Eo = 8.85x10^-12]. The complete calculations are shown in the picture attached below. 

Magnetic Properties (19th Day)

Spring 2015
Professor Mason
May 7 Class

Magnetic Field Sketch
In class, the first thing we needed to do was to draw the magnetic field using arrow around the magnet. We were given a random magnet, then we placed it on the white board. We had to determine the the direction of the arrow by using compass; the arrow points toward the north direction of the compass. After we finished the experiment, we found out that our magnet had two magnetic field, and the main point of the field was placed in the middle of the magnet as shown in the picture attached. Therefore, when we drew a continuous arrow, it would look like a butterfly.

Flux and Gauss Law Magnetism Proof
In class, we were asked to create a flux sketch based on our magnet; however, out magnet had a weird magnetic field, so we changed it to a normal magnet with normal magnetic field. Flux is defined as net number of poles enclosed divided by epsilon, [Flux = N/Eo], which would always be equal to zero. We also found out the unit of magnetic filed (B vector) is Tesla or Gauss; 1 Gauss is equal to 1/1000 Tesla. We had an interesting experiment involving magnet; first, we had a magnetized paper clip, then we cut it in half, and the result is each clip now has different pole. This also applies for the big magnet as shown in the picture above. If we break the magnet, it still has pole going on through the big magnet.



Magnetic Force
In class, we learned that most field, such as gravitational field and electric field, are part of force field; therefore, Magnetic Field is also a force field. Force of the magnetic field is perpendicular to electric field; the fun fact is that magnetic field also exists inside our brain. +Ve charge rotate clockwise, -Ve charge rotate counterclockwise. For electrons, we use left hand rule, and for protons, we use right hand rule. Magnetic force is defined as an equation of [F = qv x B], which B has a unit of kg/CS.

Magnet and Oscilloscope
We had an experiment in class, which it involved with an oscilloscope. We put a big magnet on top of the oscilloscope, then the graph on the oscilloscope changes. We also needed to draw a single beam with magnet, and we needed to draw the direction of the beam with magnet. We also needed to draw three vectors of magnetic field stated with the green dot on the oscilloscope; those three vectors are velocity, magnetic field, and force. The picture attached shows the direction of the arrow when we place a magnet on top or next to the oscilloscope depending on the north or south direction. It is also defined as [F = qVB sin theta], and [w = V/r], therefore [B = F/2pi qrf].

Magnetic Forces and Electric Current

 In class, we did an experiment involving this big magnet and a machine that supplies current.

 We put the wire in between the magnet; then when the professor turned on the machine, the wire started to make a curve downward as the magnet pulls the wire, although the wire is made of copper. The sketch shown on the picture above was the calculation of the wire when it is curving instead of a straight wire.

The picture above shows the calculation of the three vectors based on the setup experiment above, which concludes an equation of [dL = I dL x B]. 

Magnetic Force on a Current Loop.

 Next, we had an experiment involving a spinning wire around the big magnet. We first needed to predict what would happen to the wire around the magnet; we predicted that it was going to spin counterclockwise; however, it turned out to be spinning 90 degree as that position is most stable as the net Torque is equal to zero. It would spin the the magnetic field is parallel to the wire. The charge moves in circular motion, so that we had to use integral on the equation, [F= Integral of I B(x) dL] as shown in the above picture. The circle with the dot inside is defined as the Force moving out, and the cross with circle around it is defined as the Force moving towards us, [F = mV^2/r].