Voltage and Current in AC Circuit (24th Day)

Spring 2015

Professor Mason

Physics 4B

May 28 Class

Graph and Properties of AC Circuit

The first thing we learned in class was about the properties of AC circuit, as well as the Voltage vs Time graph and Current vs Time graph. In class, professor Mason showed us the form of Voltage vs Time graph in AC circuit, and it is shown in the picture attached on the left; he also showed us the form of Current vs Time graph in AC circuit; the difference between those two graphs is that Voltage vs Time graph has higher amplitude than Current vs Time graph (NOTE: the graph in the picture on the left is wrong, the top one should be I vs t, and the lower one should be V vs t because V vs t graph has higher amplitude than I vs t graph; they should be swapped). We also learned the properties of AC circuit in class, and one of those is the Voltage across resistors, which has an equation of [V = Vmax Sin(2 pi f t)] or [V = Vmax Sin(wt+flux) + Vo], and [w = 2 pi f = 2 pi/T]. We also found out an equation of current across resistors, which is [I = Imax Sin(wt + flux) - Io]. Professor told us an average value of V vs t graph (sin graph) is equal to zero; however, if this sin graph was squared, the graph becomes like the graph shown in the picture attached on the left [V=Vmax sin (2 pi/T)t]. The average value of sin squared equation is equal to cos squared equation value. We also found out that Irms and Vrms has equations of [Irms = Imax/2^1/2] and [Vrms = Vmax/2^1/2]. In class, we also learned that Average Power has an equation of [Pavg = 1/2 I^2max R], so that [Vrms = Irms R]. 

RMS and AC Current and Voltage Experiment

 After we finished learning the properties of AC Circuit in class, we continued to the experiment. This experiment's setup contains current sensor parallel to a 100 Ohm resistor, Voltage probe, function generator, and motion detector connected to logger pro. We first needed to set the frequency and voltage in function generator to 10 Hz and 3 V.

The pictures attached on the left shows how we set up the circuit, and the graph picture on the left shows us how the Current vs Time and Voltage vs Time graph would look like after we hit "Collect" button on Logger Pro based on our circuit setup. Next, we needed to find the Vmax and Imax from the graph to calculate the experimented Vrms and Irms.

After we got the graph, we needed to compare the theoretical Vrms and Irms measured from the multi meter with the experimented Vrms and Irms from the graph. They turned out to be almost the same, and the percent error turned out to be 36.4% for Irms and 1.45 % for Vrms shown in the picture attached on the right.

After we finished the experiment, we figured out a new equation, which was [Q = Integral of I dt], which would equal to [I = C dv/dt]. Based on this experiment, we also found out that Current as a function of time across capacitor has an equation of [I(t) = C Vmax w cos(wt+flux)]. The difference in amplitude in graph from V has a difference by I(t) = C w.



Capacitive and Inductive Reactance

 After we finished the calculation based on the experiment above, we continued to phase difference and Capacitive reactance and Inductive Reactance. We were given an equation of phase difference, which is [Phase diff = delta t/T], which would be used later on the next experiment. We also found out an equation of capacitive reactance, which is [Xc = 1/ cw] or [Xc = 1/2 pi f c], and also can be [Xc = Vrms/Irms], which Xc has a unit of Ohm. On the other hand, inductive reactance has an equation of [Xl = wL] or [Xl = 2 pi f L].

Experiment with 100 uF capacitor

 In this experiment, we had the exact setup and steps as the experiment with 100 Ohm resistors; the only difference is we were using 100 uF capacitor instead of resistor. The picture on the left shows us how we set up the circuit for this experiment. After we hit "Collect" button, it would show up a graph like shown in the picture on the left. The calculated Vmax, Imax, Experimented Vrms and Irms, Theoretical Vrms and Irms are shown in the picture attached below, as well as the percent error.

 This time, we needed to find the phase difference, which is the time difference between v vs t graph reach first max point and I vs t graph reach first max point divided by period; we got 0.24 as the phase difference.

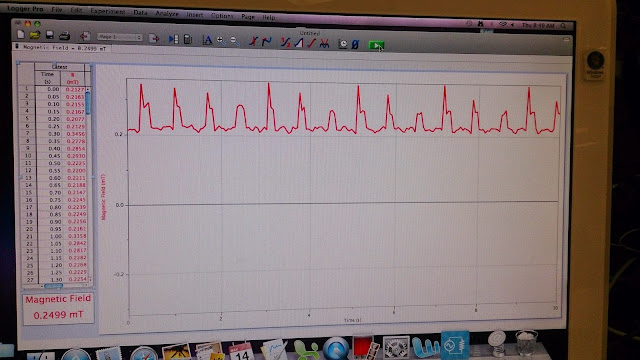
Experiment with Coil

This last experiment today was also the same as the other two experiments; however, the only difference is we used coil instead of resistor of capacitor. This time, we needed to compare this result with the previous result on previous meeting. The graph looks like this, shown in the picture attached above, when it is connected to motion detector, function generator, and probe in Logger Pro.

Phase Angle and Impedance

The last thing we learned from today's class was the formula of phase angle and impedance. Phase angle has an equation of [tan (theta) = Xl - Xc/R], while impedance has an equation of [Z = square root of R^2 + (Xl - Xc)^2], which theta is the angle for phase angle, and Z is the impedance. 

Inductance in DC Circuit (23rd Day)

Spring 2015
Professor Mason
Phys 4b
May 26 Class

Inductor Voltage and Current
The first thing in class that we learned was about Inductor Voltage and Current. An inductor is a coil of wire which stores energy in a magnetic field when it carries a current. The inductance L of an inductor is defined as the magnetic flux through the inductor per unit current. Then, we were given an equation of [L = Flux max/ i]. Any change in the current through an inductor leads to a change in the magnetic field it produces. It also will lead to a change in the magnetic flux through the inductor which, produces in induced emf in the inductor according to Faraday's Law. In the lab manual, we were given a graph of potential difference across the inductor after the switch is closed, and the voltage vs time graph is shown in the picture attached below.

The graph were measured by a tool shown in the picture above. 

The moment the switch in a circuit is closed, there is no current flowing, and the voltage across the inductor is the same as the emf of the voltage source. The current starts to increase from zero, and it changes rapidly at first, and it also levels off as it reaches its steady-state value of [epsilon/R]. The potential difference across the inductor decays exponentially with the rate of change of the current as provided with an equation of [VL = E exp(-t/Time constant)], which Time constant has a formula of [Time constant = L/R] (only applies for DC circuit). The current vs time graph is shown in the picture attached below.

This picture attached above also shows us that 100 ohm resistor has the colors of Brown-Black-Brown line on it. We were also asked to calculate the value of induction of the coil if the coil has an area of 5 by 5 centimeters and also has a length of 5 cm; we calculated it using an equation of [L = Uo N^2 A/Lo], which is shown in the picture above as 4.9x10^-2 H as the answer for that calculation. We were also asked to find the value of resistance based on a copper coil of 18H (gauge) using an equation of [R = rho L/A], which is shown in the picture above as 0.3 ohm as the answer of that calculation. 

Oscilloscope Experiment

Next in class, we needed to do an experiment on oscilloscope attached to a coil and a resistor in order to find the right current function graph. The steps to set up the oscilloscope are: 1. connect alligator clip from CH 1 across the output of the function generator, 2. set the function generator to produce a sinusoidal wave form, 3. set the triggering source to CH1, 4. Trigger on a positive slope, 5. adjust horizontal, vertical scale, position knobs, and triggering level knob, so it has a stable display of graph. The sketch of the circuit we needed in this experiment is shown in the picture below. 

In this experiment, we needed to set up a circuit attached to an oscilloscope, and the steps are as follows: 1. measure the resistance Rl of the solenoid and R of the resistor with the DMM, 2. construct the circuit as shown above assuming that the internal resistance r of the function generator is 50 ohm, 3. connect oscilloscope in parallel with the solenoid, 4. set the function generator to produce a square wave form, 5. adjust vertical and horizontal scales and positions of the oscilloscope to display the voltage across the inductor, 6. adjust frequency of the function generator, 7. measure the half-time t_1/2 of the decay of the induced emf in the solenoid, 8. determine the inductance of the coil and its uncertainty from the measurement, 9. use measured inductance to determine the number of turns N in the solenoid and uncertainty. The graph shown in the oscilloscope based on the circuit above is shown in the picture attached below.

 The picture attached below shows us how we set up the function generator, oscilloscope, resistor, and inductor(coil) based on the sketch of circuit given from the lab manual.

The calculation part of this experiment is all shown in the first picture attached at the very top of this blog; we needed to use the total R of 150 ohm because of the 100 ohm resistor added by the internal resistance of the function generator, which is 50 ohm. Then, we needed to find the period and the frequency, and they are all shown in the firs picture attached on this blog. 

The picture attached above shows us the percent error for the resistor, which is 5%; it also shows us the uncertainty for t_1/2, which is plus minus 2x10^-7 s.

Faraday's Law of Induction

Next, after we finished the oscilloscope experiment session, we continued to doing calculations on Faraday's Law of induction, which has an equation of [E = (-d Flux B/dt)N]. We were given a circuit as shown in the picture attached above, and first, we needed to calculate the time constant that has a unit of seconds shown in the picture above. Then, we also needed to calculate the voltage drop across the resistors, calculate how much time it takes from the voltage drop to exactly 11 V, calculate how much energy dissipated, calculate how much energy stored on the whiteboard using the formulas shown in the picture attached above. 

Ampere's Law, Coil, and Solenoid (22nd Day).

Spring 2015
Professor Mason
May 19 Class


Computer  Work (13.9 and 13.10)
In class, we were given several works to do on the computer. First, we had to type "active physics" on Google, then click on "University Physics," which has a link: (http://wps.aw.com/aw_young_physics_11/). We first need to pick part IV Electromagnetism; to do that, we need to click the bar at the top left corner and switch it to electromagnetism. First, we had to do 13.9, which is the electromagnetic induction. This picture attached below shows us the questions provided on section 13.9 as well as the magnetic flux simulation to play with in order to help us finish all the questions.

The answers for each question on section 13.9 are shown in the picture attached below.

In the beginning of class, we also were given some equations of [E = d(flux . B)/dt], [Flux B = Integral of B vector dA or Integral of B vector cos(theta) dA], and the last one was [E = -N(d Flux/dt or E = -N(d BA cos(theta)/dt)]. While we were doing this computer work, professor Mason showed us an experiment with big magnet and rod. The diagram of where the magnetic field and the force of the rod is going is shown in the picture above; the experiment is shown in the picture attached below. 

With the power supply attached to the experiment tool, we could set up the rod as much as we wanted to; for example, we could either make the rod move towards the big magnet or make the rod move away from the big magnet depending on how the professor set the power supply. 

After we finished computer work section 13.9, we continued on doing section 13.10, which is shown in the picture attached below. 

 The picture above shows a Motional EMF simulation for section 13.10, which is the Motional EMF; as well as the simulation in section 13.9, we could play with this simulation as well, such as adjusting the length, resistance, magnetic field, and velocity; we could also choose which graph would it provide for us (I E and flux).

 The answers for section 13.10 are shown in the picture attached above, except for question 13; question 13's answer is shown in the picture attached below. Based on the picture above, we found out an equation of [Induction I = -BLV/R].

Inductions Properties

 In this class section, we learned some things about inductions and inductor; one thing we found out about inductors is that inductors function like capacitors, but it stores energy by the magnetic field. We also learned that as V increases, I decreases; as B increases, back emf also increases; as number of coils increases, R also increases; finally, the bigger the coil, the bigger the resistance is.

 We also found out some new equations, and one of them is [C = Q/V = I(dB/dt)/V]; that equation comes from the three equations of Voltage, which are [V = L(dI/dt)], [V=IR], and [V = I(dB/dt)/C]. We were also given an equation for B solenoid, which is [B solenoid = Vo I (N/L)].

In the middle of the class, we were asked to do some calculations for induction of coil; therefore, we needed to use an induction of coil formula, which is [L = Uo N^2 A/ Lo (dI/dt)], which Uo is a constant of 1.25x10^-6, and L has a unit called "Henry." We also learned that there are ways to decrease and increase inductions in coil. Ways to decrease inductions are: 1. Reduce the distance of plates, and 2. put something in between the plates; ways to increase inductions are: 1. increase the area of plates, 2. increase the length, 3. increase the loop, and 4. increase the Uo permibility (insulator). Based on the picture attached above, we learned that inductor acts like nothing in a wire or coil (dI/dt = 0). 

Another Computer Work (14.1)

After we finished doing some calculations on inductions, we continued on doing the computer work section 14.1, which is the RL circuit. Similar to section 13.9 and 13.10, this section 14.1 also has a simulation called RL circuit simulation to play with. This time, we can adjust the R, L, and V in order to help us finish all the question through this section. The simulation is shown in the picture attached below. 

 The answers for section 14.1 are shown in the picture attached above.

For question #2, we took a picture of the answers on computer because we need the detailed answer, and it is shown in the picture attached above. For this questions, we learned that Faraday's Law states that if the magnetic flux through a region of space changes, an electromotive force, or EMF, is induced in the region. The direction of the induced EMF is such that if charge is present in the region, the EMF will drive the charge to create magnetic flux in opposition to the original change in magnetic flux. The magnitude of the induced EMF is proportional to the rrate of change of magnetic flux. 

For question #8, this is how we got 1.7 A through some calculations, and it is shown in the picture attached above. Based on this computer work section 14.1, we learned that if we double the inductance, the time increases, and if we double the resistance, the time decreases. Based on this work, we also learned that Time constant is perpendicular to 1/L; if Time constant equals to 0, it means that it is going slow; if Time constant equals to infinity, it means that it is going fast. In conclusion for this work, the formula we need to know is [Time constant = L/R]. 

Magnetic Field, Loop, and Faraday (21st Day)

Spring 2015

Professor Mason

May 14 Class

Magnetic Field on Wire

First thing in class, we needed to predict and draw the direction of magnetic field including the force and which direction the magnetic field is pointing at 4 location shown in the picture below. To calculate the force, we use this formula [F vector = B vector I L vector], or [F vector = (Uo I1 I2/ 2pi r) L vector], which r is the distance between two wires. Since B is perpendicular to I, we could also say that [B vector = Uo I1 I2/ 2pi r]. 

If a magnetic field on the axis of loops has a straight line wire that gives us circular magnetic field, circular wire gives us straight line magnetic field. The picture shown above also shows a B vector graph when B vector sensor is spun around the classroom (similar to wave graph); the highest point of the graph shows the north direction, while the lowest point of the graph shows the south direction. The picture attached below shows us the experiment with the wire. We were also asked if there was any force acting on the wire shown in the picture below; the answer is no, there is no force between the wires because the direction of the current is going back and forth, therefore they cancel each other out. 

Experiment With Magnetic Field on Logger Pro.
Next, we had an experiment, which involved a power supply, test tube, copper wire, magnetic field reader, and alligator clips. The setup is shown in the picture below. In this experiment, we needed to determine how the graph of magnetic field would look like on logger pro based on how many loops encircling the test tube. We had to put the magnetic field reader close to the test tube, so that it would read accurately. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 1 and 1 loop encircling the test tube.

 The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 1 and 2 loop encircling the test tube.

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 1 and 3 loop encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 1 and 4 loop encircling the test tube.

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 1 and 5 loop encircling the test tube. 

After we were done with power supply 1, we noticed that the big difference only lies in 1 loop and 2 loops; the rest of loops did not have much of a difference than 2 loops encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 2 and 1 loop encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 2 and 2 loop encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 2 and 3 loop encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 2 and 4 loop encircling the test tube. 

The picture below shows the magnetic field graph of B vs T on Logger Pro with Power Supply 2 and 5 loop encircling the test tube. 

When using power supply 2 (shown in the picture below), we noticed from 1 loop to 5 loops, the differences are the Magnetic Field (B); the graph increases the height as we added more loops encircling the test tube.

Galvanometer

In class, we were shown this old machine called Galvanometer as shown in the picture attached above. It is used to detect current and give an analogous reading. In this experiment, there was a  loop of wire attached up to the galvanometer, and it showed 0 A because there was no current at this point of time. The professor then took a bar of magnet and placed it into the center of the loop of wire. The galvanometer then suddenly started for a second to give a reading of some current. After he pulled it out, the galvanometer would get another reading; however, this time the galvanometer gave a negative direction. The professor then did the experiment again; however, this time he moved the bar of magnet back and forth in the center of the loop at higher speed. After that, the galvanometer received a higher reading of the magnitude of the current flowing within the wire. From this experiment, we could conclude that magnetic field can generate wireless current.

Faraday's Machine

In class, we get to see a Faraday's machine. The professor told us four things that are important in using the Faraday's Machine, and those are the strength of the magnet, the velocity of magnet's entry and exit, the radius of loop coil, and number of coils. 

The first thing he put in the Faraday's machine in this experiment was a coil with light bulb attached. Then, the bulb lights up when it is in the pole. 

The bulb did not light up again after the coil is released from the pole. 

In this experiment, the professor also provided us a copper ring, aluminum ring, steel ring, and special steel ring (has a gap in between the disk); however, we did not take pictures of them; thus we knew how they worked. First, when the professor put the copper ring inside the pole, it levitated slightly upward; next, when the professor put the aluminum ring inside the pole, it levitated higher than copper ring because aluminum is lighter than copper; next, when the professor put steel ring inside the pole, it levitated as high as copper; however, when the professor put a special steel ring in the pole, it did not levitate at all because the magnetic field was interrupted by the gap between the disk, so it did not make any circular motion. After the experiment, the professor came up with another equation, which was motion EMF [E = VB] or [E vector = V/L] or [E vector = V L B vector]. 

Falling Experiment

In class, professor did another experiment with two objects; one is magnetic and the other one is not. He also prepared two tubes; one is made of plastic glass, and the other one is made of aluminum. He purposely drop two objects at the same time through different pole. The magnetic object going through the aluminum tube fell down so much slower than the other one because the object is spinning in circular current; however, it did not stop because the gravity is pulling the object down, and it needed to move to fall down.

After the experiment, the professor came up with another equation of [E = -NA (dB/dt)] or [E = N (d(B vector dot A vector)/ dt)], which E is Lenz's Law (Induced EMF) using [Magnetic Flux = B.A]. Then, the professor gave us another equation of [B = Bo Sin wt], [Flux = pi R^2 Bo Sin wt], and [E = -Npi R^2 Bo Cos wt]. These equations are used to find the flux in a coil as function of time. Next, we also needed to draw emf vs t graph based on B vs t graph; the result looks like the graph shown in the picture attached below.